Geometry for Feynman’s Lectures Exercises 2.24

Solving this exercise via force components is straightforward, leading to the answer $x$. However, I struggled with solving it using the principle of virtual work.

The hardest part of this exercise was calculating how the weight moves when we displace the cart. For simplicity, I reflected the diagram horizontally, aligning the movement with the standard x-axis.

One important point is that we cannot simply multiply the displacement by $^$, as this does not account for the fact that the weight moves along a circular path due to the rope.

I arrived at the following diagram, and the solution became clear from its geometry. In this diagram, the card moves to the right and $AB = x$.

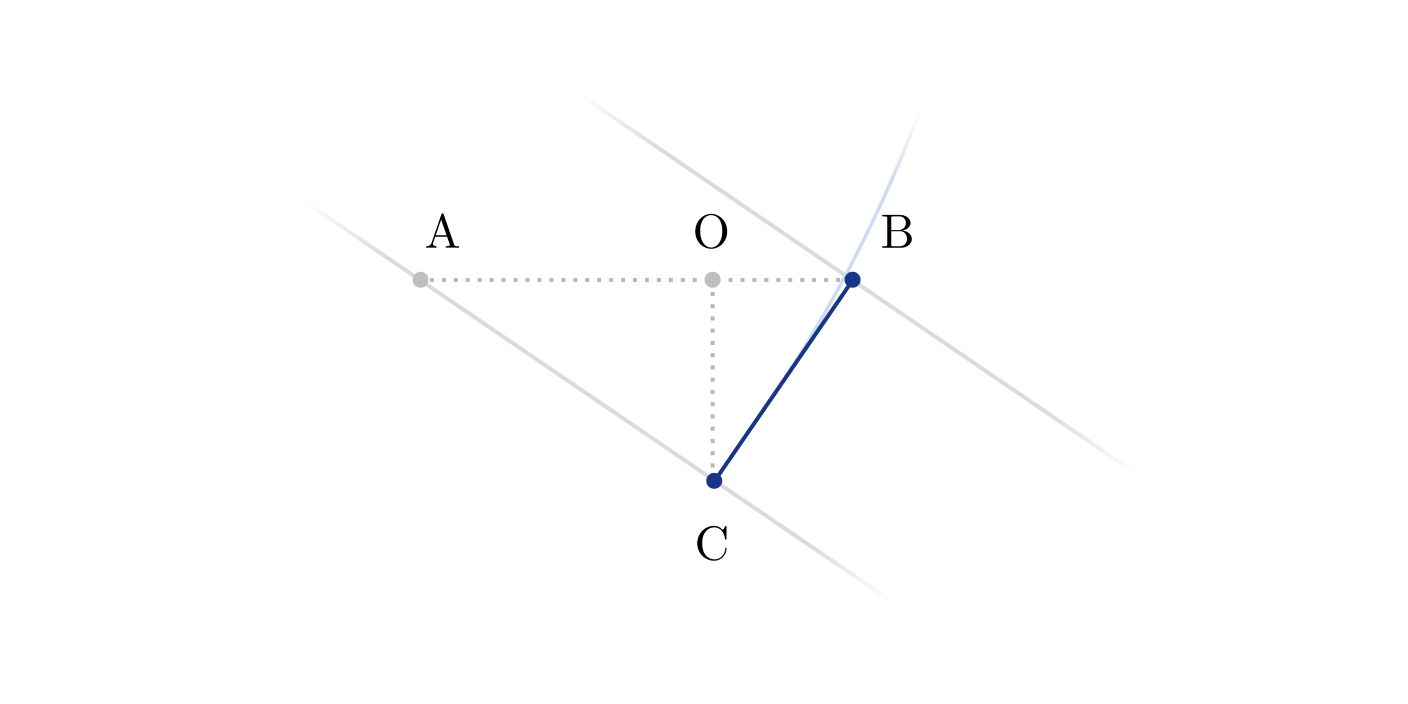
We can approximate the path of the weight by a straight line, as the angle of the rope will be small. Thus, we obtain:

${\displaystyle \mathrm{\angle }ACB=90^{\circ }⟹AC=AB\cdot \cos 30^{\circ }=\mathrm{\Delta }x\cdot \cos 30^{\circ }}$

Finally, we arrive at the correct answer:

${\displaystyle \mathrm{\angle }AOC=90^{\circ }⟹OC=AC\cdot \sin 30^{\circ }=\mathrm{\Delta }x\cdot \cos 30^{\circ }\cdot \sin 30^{\circ }}$

I would be interested in solving this analytically by equating the equation for a circle with that of the plane to find the coordinates of the point. Ultimately, for the principle of virtual work, we only need to determine $\frac{\delta y}{\delta x}$.

If anyone stumbles upon this post and finds such a solution, please feel free to send a copy to $@$.

Eiermann Desk

Last year I was looking for a new desk. My main requirement was that it should be lower than 70 cm. Most desks today are 75 cm high, which is too tall for most people. I also wanted to avoid the Silicon Valley vibe that is so ubiquitous in modern workspaces.

Eventually, I found the table I loved — the Eiermann 1. The original table frame was designed in 1953, either for Eiermann’s own office or for his students; history differs on this point. The crossbar, made in one piece, is placed diagonally between the sides. This reduced construction achieves the perfect balance between material and stability. The tabletop lies flat on the frame. Less is not possible.

It’s been almost a year and it still brings me joy every time I sit at it.

It’s been almost two months since I bought Feynman’s exercises. I didn’t expect physics to capture my attention this much. I’ve finished six chapters and created 200 new Mochi cards since then.

The exercises turned out to be the key to understanding. There were many times when I read a chapter, thought I understood it, but then found myself lost when trying to solve a practical problem. There must be a reason for this phenomenon. My guess is that it’s easy to confuse familiarity with understanding. Reading gives you the sense of the tools you can use, but it doesn’t teach you how to use them.

Doing exercises highlighted how much I’ve forgotten from mathematics. As a refresher, I skimmed through Lang’s Basic Mathematics. I started going through Spivak’s Calculus, which has even more exercises than the Feynman’s books.

This experience makes me wonder how it’s possible to cover everything in university. Sometimes I spend days thinking about a single problem. I don’t know if you can afford that when you have other subjects to study.

Turkey ’24

We just returned from Turkey, where we spent a week on a sailing boat and added the first 175 miles to our logbooks.

This might be the best vacation I’ve ever had. I’ve been thinking about what made it so, and the answer seems to be that sailing is wonderfully unpredictable. With few specific arrangements beyond where you’ll dock, it felt more like an adventure than a traditional vacation. The best trips I’ve taken have been like this.

Recently 003

I’m still working through the exercises to the Feynman’s Lectures. There are 36 of them to the Chapter 4! Doing exercises turned out to be the best way to understand something. I want to move forward faster with lectures and I have to stop myself constantly. It’s easy to fool yourself and think you understand the material after reading a lecture, only I open a new exercise and realize that there are gaps.

Mochi helps a lot. It’s surprising that this isn’t taught in schools and universities. Spaced repetition might be the only reliable and proven way to enhance memory. As Michael Nilsen says, “Anki makes memory a choice, rather than a haphazard event, to be left to chance.” It feels like superpower.

Movies watched

• First Man. Damien Chazelle brought depth to the story and focused on personal drama, stepping away from all the stories surrounding a well-known person.
• Oppenheimer. I rewatched it again with subtitles this time. It was better. Still, this movie lacks complexity and depth.
• Flow. An indie animation without any dialogues and with interesting style (probably shaped by its budget).
• The Wild Robot. As someone on Letterboxd put it, “the best Pixar cartoon was made by Dreamworks”. It’s an overstatement, but it’s a good cartoon.

Reading

Finished reading Bullshit Jobs. It resonated with my thoughts that many modern jobs are mind-numbing, and many more make the world a worse place. Still, it was quite repetitive and could’ve been half its size.

Dropped The Invention of Science after a few chapters. This turned out not to be a history of inventions, but more a philosophical work on how that was happening — how people talked and thought about it. It might be good, but it wasn’t what I expected.

Currently reading The Life of Isaac Newton, which has been good so far.

The easiest way to solve 2.19 (Plank Weight Trough)

A plank of weight W and length $R$ lies in a smooth circular trough of radius $R$. At one end of the plank is a weight $W/2$. Calculate the angle $\theta$ at which the plank lies when it is in equilibrium.

There are already a few solutions at the Feynman’s Lectures website, but my solution is simpler.

Since the plank is in equilibrium, it must be at its lowest possible position. This means the center of mass of the plank lies directly below the center of the trough.

We can calculate the center of mass $c$ given the length of the plank $L = R$:

${\displaystyle \begin{array}{rl}{\displaystyle c}& {\displaystyle =\frac{1}{1.5W}(\frac{WL}{2}+\frac{WL}{2})}\\ {\displaystyle }& {\displaystyle =\frac{L}{1.5}=\frac{\sqrt{3}R}{1.5}=\frac{2R}{\sqrt{3}}}\end{array}}$

Since $c$ forms the hypotenuse from the left point of contact to the vertical line beneath the trough center, we have:

${\displaystyle \cos \theta =\frac{R}{c}=\frac{R\sqrt{3}}{2R}=\frac{\sqrt{3}}{2}}$

This gives $= 30^{}$