Geometry for FLPE 2.24

Solving this exercise via force components is straightforward, leading to the answer $x$. However, I struggled with solving it using the principle of virtual work.

The hardest part of this exercise was calculating how the weight moves when we displace the cart. For simplicity, I reflected the diagram horizontally, aligning the movement with the standard x-axis.

One important point is that we cannot simply multiply the displacement by $^$, as this does not account for the fact that the weight moves along a circular path due to the rope.

I arrived at the following diagram, and the solution became clear from its geometry. In this diagram, the card moves to the right and $AB = x$.

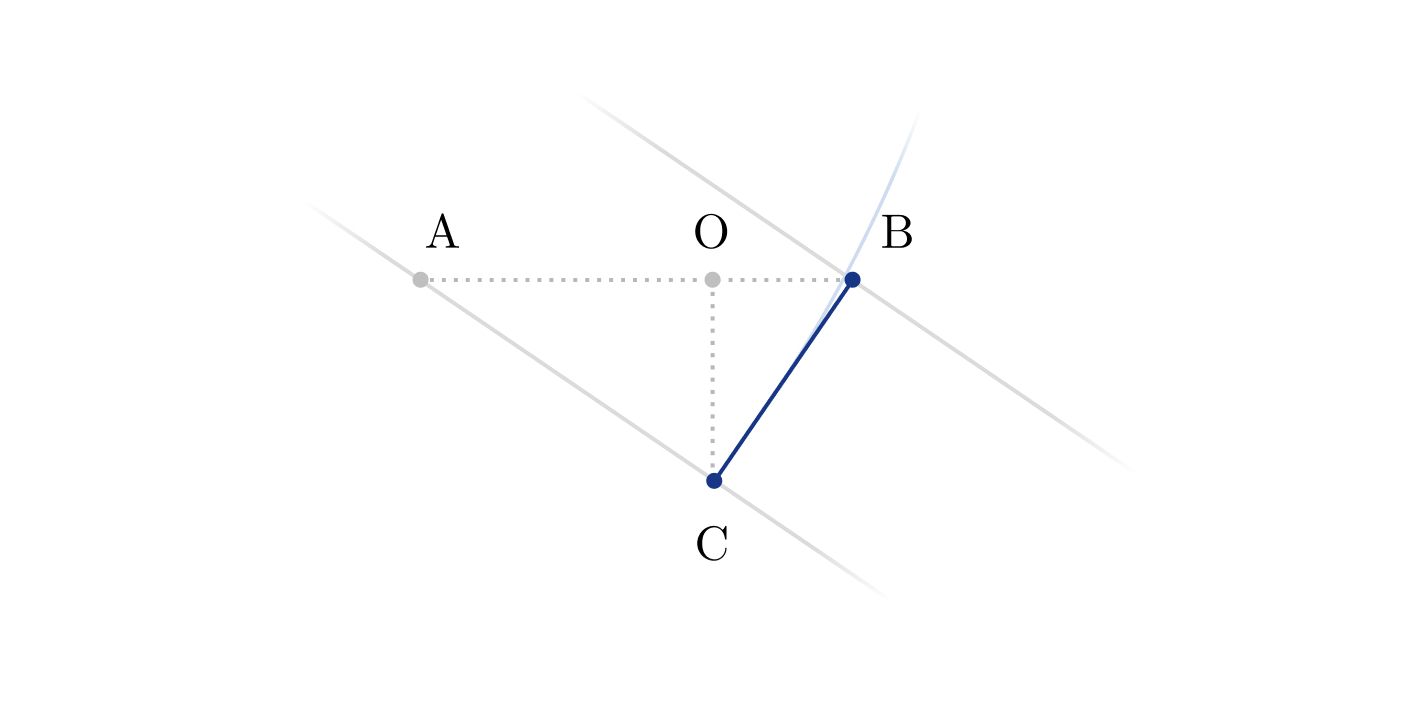
We can approximate the path of the weight by a straight line, as the angle of the rope will be small. Thus, we obtain:

${\displaystyle \mathrm{\angle }ACB=90^{\circ }⟹AC=AB\cdot \cos 30^{\circ }=\mathrm{\Delta }x\cdot \cos 30^{\circ }}$

Finally, we arrive at the correct answer:

${\displaystyle \mathrm{\angle }AOC=90^{\circ }⟹OC=AC\cdot \sin 30^{\circ }=\mathrm{\Delta }x\cdot \cos 30^{\circ }\cdot \sin 30^{\circ }}$

I would be interested in solving this analytically by equating the equation for a circle with that of the plane to find the coordinates of the point. Ultimately, for the principle of virtual work, we only need to determine $\frac{\delta y}{\delta x}$.

If anyone stumbles upon this post and finds such a solution, please feel free to send a copy to $@$.