Solving 2.17 and 2.18 Using the Principle of Virtual Work

It is possible to solve 2.17 and 2.18 using torques, but since the chapter was about using the virtual work principle, let’s use it.

Let’s consider the ladder from the exercise 2.18 (2.17 uses similar approach) rotating clockwise due to the reactive force of the wall.

Let’s imagine a ladder rotating clockwise under the influence of the reaction force of the wall. As the ladder rotates by a small angle $\delta \theta$ radians, it displaces a distance $s = r$ (by the definition of a radian).

For a small angle $\theta$, it is possible to approximate that any point on ladder moves in a straight line, not in a circular path (see figure below).

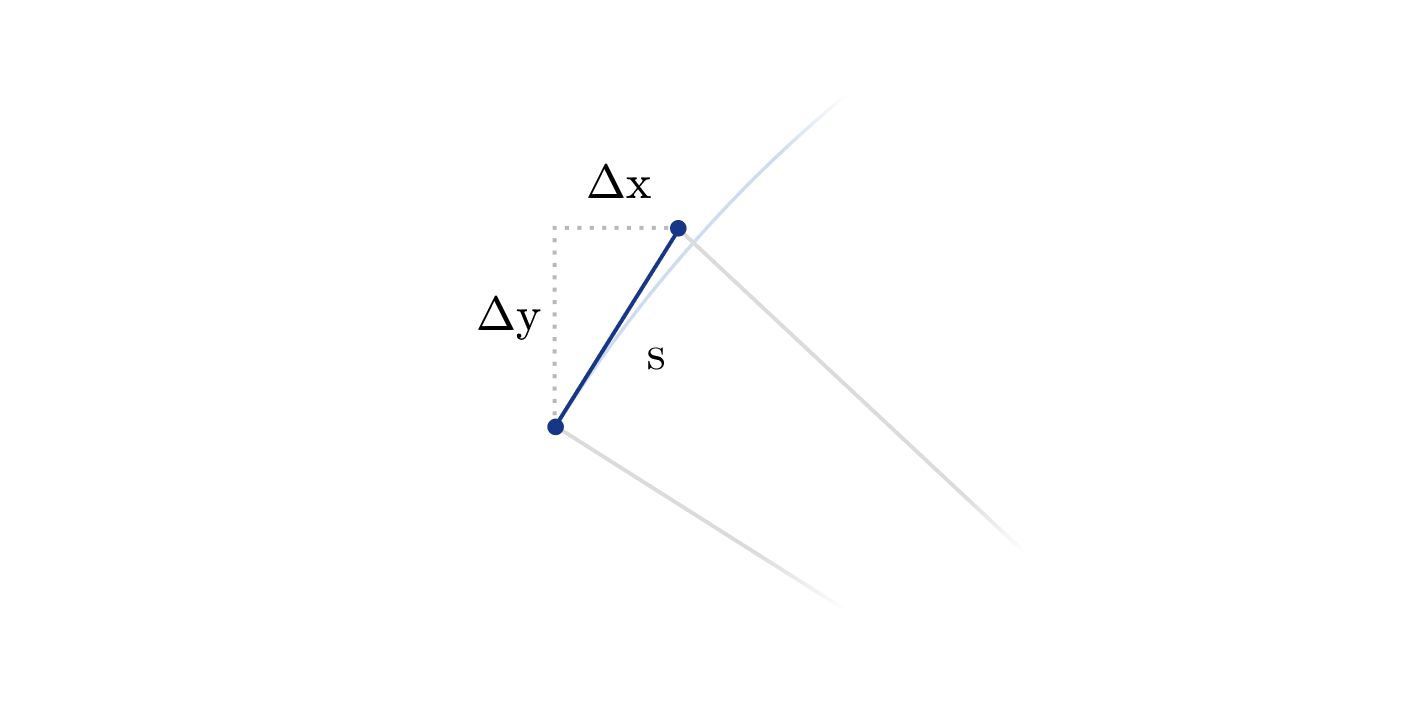
This linear movement allows us to compute displacement of each point on the ladder as the following:

${\displaystyle \begin{array}{rl}{\displaystyle \mathrm{\Delta }x}& {\displaystyle =s\sin \theta =\delta \theta \cdot r\cdot \sin \theta }\\ {\displaystyle \mathrm{\Delta }y}& {\displaystyle =s\cos \theta =\delta \theta \cdot r\cdot \cos \theta }\end{array}}$

Now we can calculate the work done by a reactive force of the wall $T$:

${\displaystyle W_T=T(\delta \theta \cdot L\cdot \sin \theta )}$

Changes in potential energies of the weight $W$ and the ladder $\omega$ are:

${\displaystyle \begin{array}{rl}{\displaystyle E_W}& {\displaystyle =(\delta \theta \cdot 0.75L\cdot \cos \theta )\cdot W}\\ {\displaystyle E_{\omega }}& {\displaystyle =(\delta \theta \cdot 0.5L\cdot \cos \theta )\cdot \omega }\end{array}}$

Equating the work done by $T$ to the total change in potential energy yields:

${\displaystyle \begin{array}{rl}{\displaystyle T(\delta \theta \cdot L\cdot \sin \theta )}& {\displaystyle =(\delta \theta \cdot 0.5L\cdot \cos \theta )\cdot \omega }\\ {\displaystyle }& {\displaystyle +(\delta \theta \cdot 0.75L\cdot \cos \theta )\cdot W}\end{array}}$

${\displaystyle T=\mathrm{ctg}\theta (0.5\omega +0.75W)}$